I recently watched the 2 part workshop (part 1, part 2) on ggplot2 and extensions given by Thomas Lin Pedersen. First of, it was really nice of Thomas to give the close to 4 hour workshop for the benefit of the community. I personally learnt a lot from it. I wanted to try out gganimate extension that was covered during the workshop.
There are several resources on the web that show animations/illustrations of proofs of mathematical identities and theorems without words (or close to it). I wanted to take a few of those examples and use gganimate to recreate the illustration. This was a fun way for me to try out gganimate.
Example 1:
This example is taken from AoPS Online and the result is that sum of first \(n\) odd numbers equals \(n^2\).
\[ 1 + 3 + 5 + \ldots + (2n - 1) = n^2 \]
The gganimate version of the proof (using the method in AoPS Online) is shown below (R code, html file)
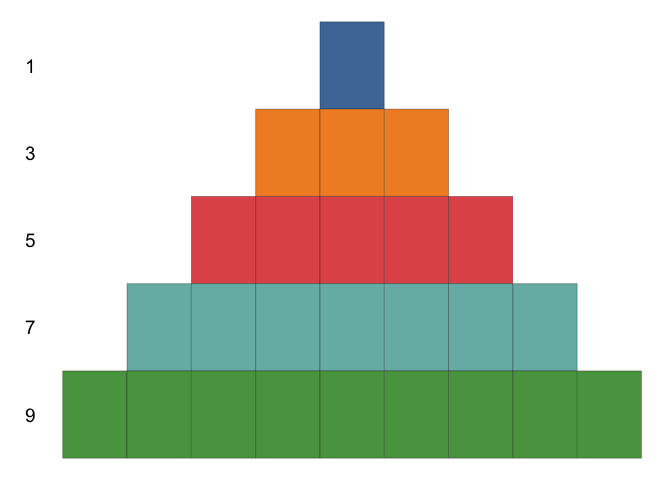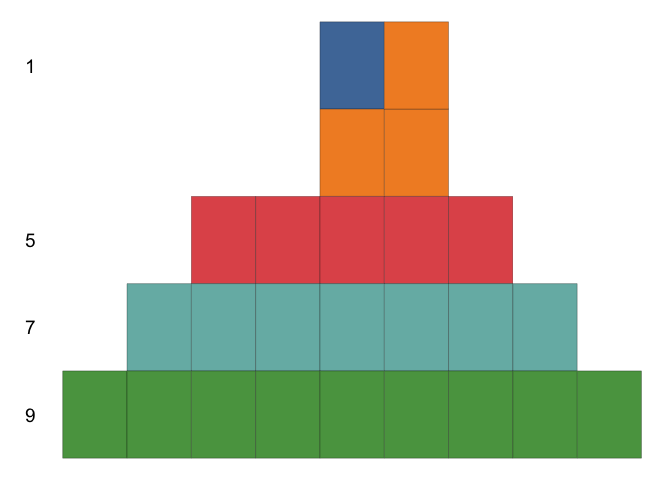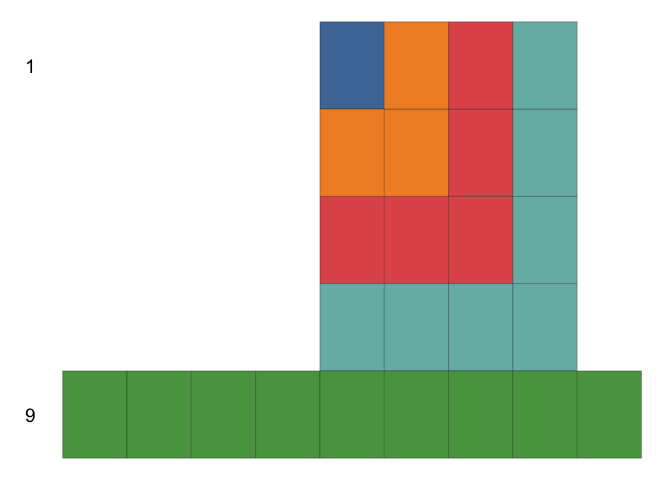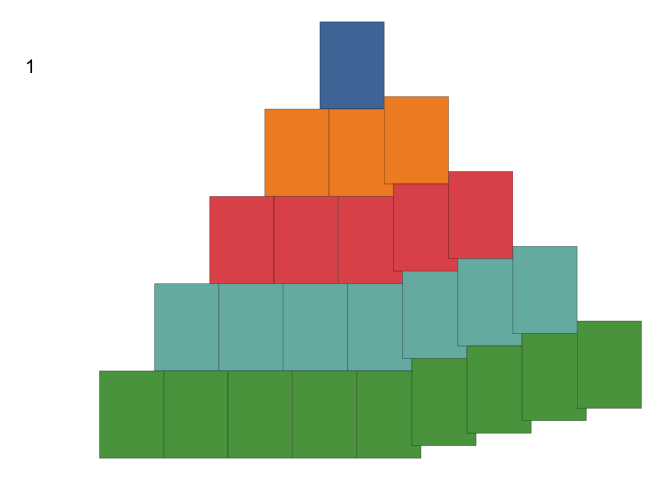
Example 2:
This example is also taken from AoPS Online and the result is:
\[ 1^3 + 2^3 + \ldots + (n-1)^3 + n^3 = (1 + 2 + \ldots + n)^2 \]
The gganimate version of the proof (using the method in AoPS Online) is shown below ( R code, html file):
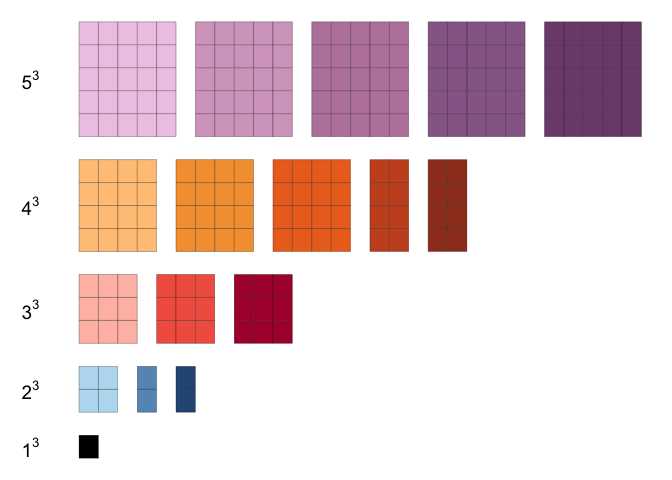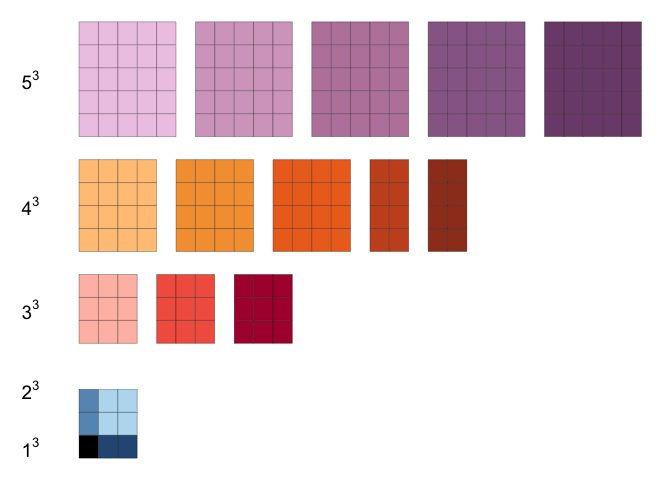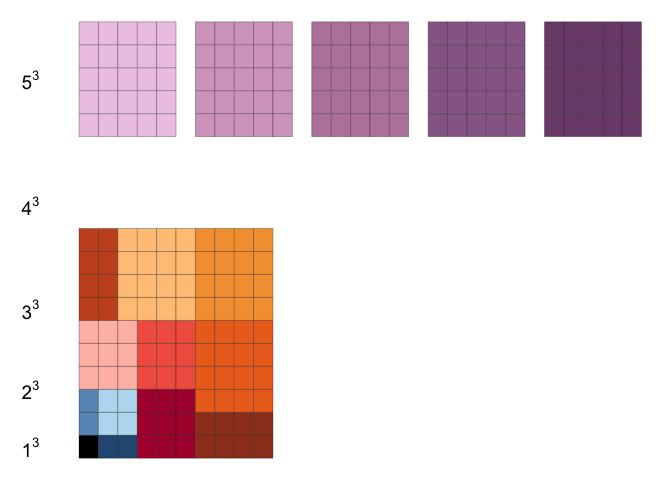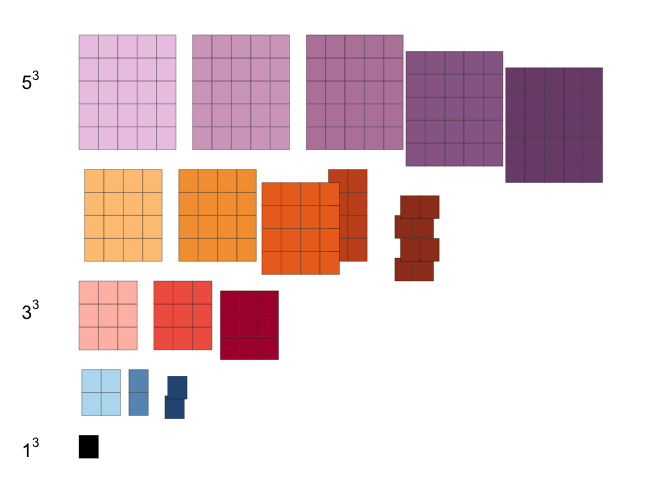
Example 3
This example from AoPS Online illustrates the result
\[ \frac{1}{2^2} + \frac{1}{2^4} + \frac{1}{2^6} + \frac{1}{2^8} + \ldots = \frac{1}{3} \]
The gganimate version of the proof (using the method in AoPS Online) is shown below ( R code, html file):
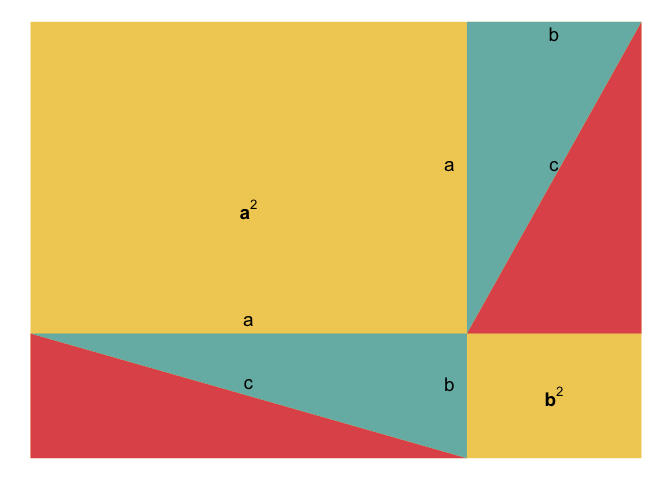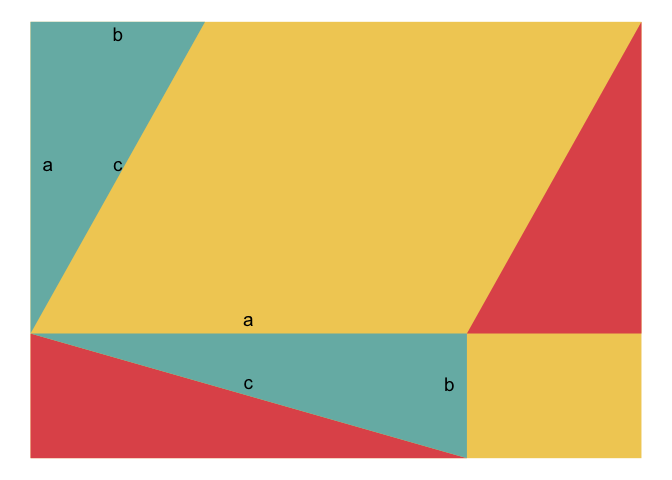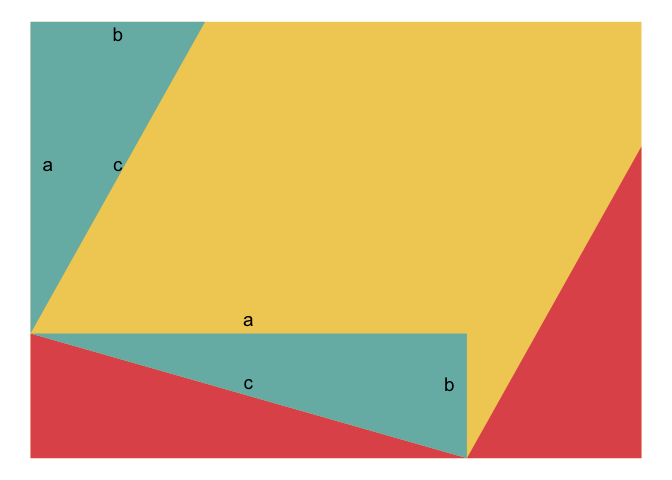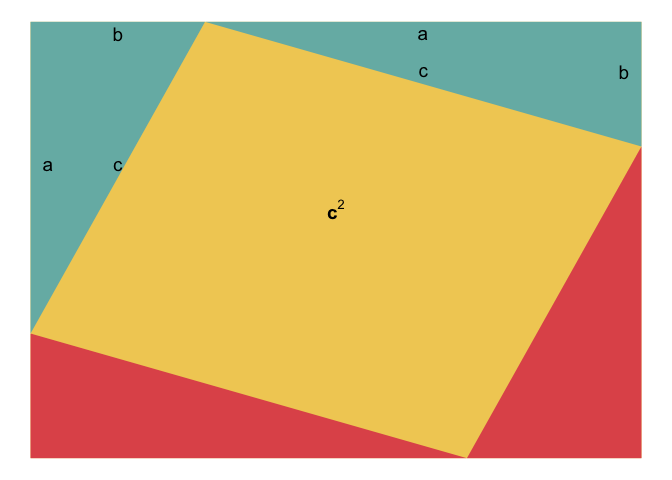
Example 4
According to Pythagoras theorem, \[ a^2 + b^2 = c^2 \] where \(a\), \(b\), \(c\) are sides of a right angled triangle (with \(c\) being the side opposite \(90^o\) angle)
There was an illustration of the proof of pythogoras theorem in a video from echalk.
The gganimate version of the proof is shown below ( R code, html file)
In summary, it was great to use gganimate for these animations since it does all the magic with making transitions work nicely.